Given
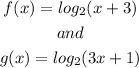
a)
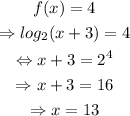
The answer to part a) is x=13. The point on the graph is (13,4)
b)
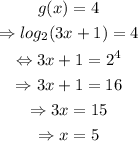
The answer to part b) is x=5, and the point on the graph is (5,4).
c)
![\begin{gathered} f(x)=g(x) \\ \Rightarrow log_2(x+3)=log_2(3x+1) \\ \Rightarrow(ln(x+3))/(ln(2))=(ln(3x+1))/(ln(2))] \\ \Rightarrow ln(x+3)=ln(3x+1) \\ \Rightarrow x+3=3x+1 \\ \Rightarrow2x=2 \\ \Rightarrow x=1 \\ and \\ log_2(1+3)=log_2(4)=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mx7ezbhxksla1xngx8dstt69gz7k655je8.png)
The answer to part c) is x=1 and graphs intersect at (1,2).
d)
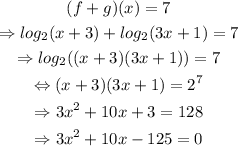
Solving the quadratic equation using the quadratic formula,
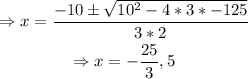
However, notice that if x=-25/3,
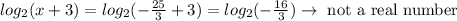
Therefore, x=-25/3 is not a valid answer.
The answer to part d) is x=5.
e)
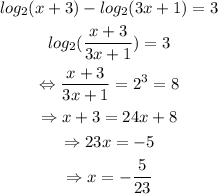
The answer to part e) is x=-5/23