Question

The following table shows a company's annual income over a 6-year period. The equation y=60000(1.2)x describes the curve of best fit for the company's annual income (y). Let x represent the number of years since 2001.

Answer 1

Given that the annual income of a company over a 6-year period is described by the equation:

`\begin{gathered} y=60000(1.2)^x \\ \text{where} \\ x\text{ is the number of years since 2001} \end{gathered}`

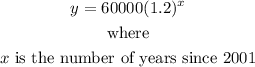
The annual income at the end of each year since 2001 is as shown in the table below:

Required: To evaluate the company's approximate annual income in 2009.

Solution:

Given the annual income described as

`y=60000(1.2)^x`

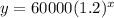
The number of years between 2001 and 2009 is evaluated as

`x\text{ = 2009 -2001 = 8 years}`

thus, it's been 8 years since 2001.

The annual income in 2009 is thus evaluated by substituting 8 for the value of x in the annual income function.

This gives

`\begin{gathered} y=60000(1.2)^x \\ x\text{ = 8} \\ \text{thus,} \\ y\text{ = 60000}*(1.2)^8 \\ =\text{ 60000}*4.29981696 \\ y=\text{ }257989.0176 \\ \Rightarrow y\approx258000 \end{gathered}`

Hence, the company's approximate annual income in the year 2009 will be $ 258000.

The third option is the correct answer.