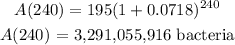Question

What was the initial population at time t=0?Find the size of the bacterial population after 4 hours.

Answer 1

Answer;

`\begin{gathered} a)\text{ 195 bacteria} \\ b)\text{ 3,291,055,916 bacteria} \end{gathered}`

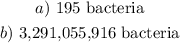
Explanation;

a) We want to get the initial population of the bacteria

We start by writing a formula that links the initial bacteria population to a later bacteria population after time t

`A(t)=I(1+r)^t`

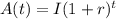
where A(t) is the bacteria population at time t

I is the initial bacteria population

r is the rate of increase in population

t is time

Now, let us find r

At t = 10; we know that A(t) = 2I

Thus, we have it that;

`\begin{gathered} 2I=I(1+r)^(10) \\ (1+r)^(10)\text{ = 2} \\ 1+r\text{ = 1.0718} \\ r\text{ = 1.0718-1} \\ r\text{ = 0.0718} \end{gathered}`

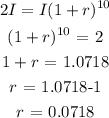
Now, let us find I, since we have r. But we have to make use of t= 80 and A(t) = 50,000

Thus, we have;

`\begin{gathered} 50,000=I(1+0.0718)^(80) \\ I\text{ = }(50,000)/((1+0.0718)^(80)) \\ I\text{ = 195} \end{gathered}`

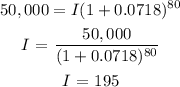
The initial population is 195 bacteria

b) For after 4 hours, we have to convert to minutes

We know that there are 60 minutes in an hour

So, in 4 hours, we have 4 * 60 = 240 minutes

Now, we proceed to use the formula above with I = 195 and t = 240

We have that as;

`\begin{gathered} A(240)=195(1+0.0718)^(240) \\ A(240)\text{ = 3,291,055,916 bacteria} \end{gathered}`