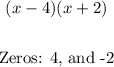Question

Factor bofe problems using synthetic division and list All zeros

Answer 1

Given:

`f(x)=x^3-7x^2+2x+40;\text{ x -5}`

Let's factor using synthetic division.

Equate the divisor to zero:

x - 5 = 0

x = 5

List all terms of the polynomial: 1, -7, 2, 40

Palce the numbers representing the divisor and dividend into a long division-like configuration

To factor using synthetic division, we have:

Therefore, the factored expression is:

`\begin{gathered} 1x^2-2x-8 \\ \\ =x^2-2x-8 \\ \\ =(x-4)(x+2) \end{gathered}`

The zeros are also the roots of the polynomial.

The zeros of a polynomial are all the x-values that makes the polynomial equal to zero,

To find the zeros, equate each afctor to zero:

(x - 4) = 0

x = 4

(x + 2) = 0

x = -2

Thus, the zeros are:

x = 4, -2

ANSWER:

`\begin{gathered} (x-4)(x+2) \\ \\ \text{Zeros: 4, and -2} \end{gathered}`