Question

9.5.35 Assigned Media An architect designs a rectangular flower garden such that the width is exactly two-thirds of the length. If 300 feet of antique picket fencing are to be used to enclose the garden, find the dimensions of the garden What is the length of the garden? The length of the garden is

Answer 1

• The dimensions of the garden are 90 feet by 60 feet.

,

• The length of the garden is 90 feet.

Step-by-step explanation:

Let the length of the garden = l

The width is exactly two-thirds of the length, Width = (2/3)l

If 300 feet of antique picket fencing are to be used to enclose the garden, this means that the perimeter of the proposed garden is 300 feet.

`\begin{gathered} \text{Perimeter}=2(\text{Length}+\text{Width)} \\ 300=2(l+(2)/(3)l) \end{gathered}`

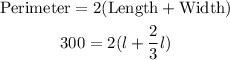
Next, solve the equation for the length, l:

`\begin{gathered} (300)/(2)=l+(2)/(3)l \\ 150=(5l)/(3) \\ l=150*(3)/(5) \\ l=90\text{ feet} \end{gathered}`

The length of the garden is 90 feet.

Next, we determine the width.

`\begin{gathered} \text{Width}=(2)/(3)l \\ =(2)/(3)*90 \\ =2*30 \\ =60\text{ feet} \end{gathered}`

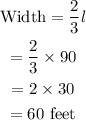
The dimensions of the garden are 90 feet by 60 feet.