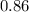Step-by-step explanation:
The total number of students is
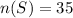
Concept:
To figure out the probability that a student earns grade A,B or C
Will be calculated below as
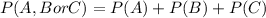
The Probability of A is
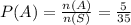
The probabaility of B is
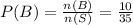
The probabaility of C is
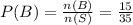
Hence,
By substituting the values in the concept, we will have
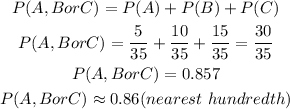
Hence,
The final answer is