The equation of a parabola in standard form is
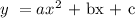
So, we have the following equations,
For ( 2, -20) , -20 = a(2)^2 + b (2) + c,
For (-2, -4), -4 = a( -2)^2 + b (-2) + c,
For (0.-8), -8 = a (0) + b (0) + c
Then solving,
4a + 2b + c = -20 .............. equ 1
4a - 2b + c = -4 ................... equ 2
c= -8
put c= -8 in equ 1,
we have
4a + 2b -8 = -20 = 4a + 2b = -12 ------equ 3
put c= -8 in equ 2,
4a - 2b -8 = -4 = 4a - 2b = 4................... equ 4
Solving equ 3 and equ 4, a= -1 , b= -4
so a =-1, b= -4, c= -8
Then substituting the values in
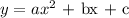
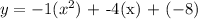
So, y= -x^2 -4x-8