Question

A company estimates that that sales will grow continuously at a rate given by the functions S’(t)=15e^t where S’(t) Is the rate at which cells are increasing, in dollars per day, on day t. find the sales from the 2nd day through the 6th day (this is the integral from one to six)

Answer 1

Given the function:

`S^(\prime)(t)=15e^t`

Where S’(t) Is the rate at which sales are increasing (in dollars per day). To find the sales from the second day through the 6th day, we need to integrate this function from t = 1 to t = 6:

`\int_1^6S^(\prime)(t)dt=\int_1^615e^tdt=15\int_1^6e^tdt`

We know that:

`\int e^tdt=e^t+C`

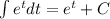
Then:

`15\int_1^6e^tdt=15(e^6-e^1)\approx\text{\$}6010.66`

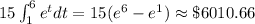
The sales from the 2nd day through the 6th day are $6,010.66