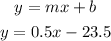Solution
Note: The formula to use is

Where m and b are given by
the b can also be given as
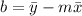
The table below will be of help
We have the following from the table
![\begin{gathered} \sum_^x=666 \\ \sum_^y=106.5 \\ \operatorname{\sum}_^x^2=39078 \\ \operatorname{\sum}_^xy=6592.5 \\ n=10 \end{gathered}]()
Substituting directing into the formula for m to obtain m

to obtain b
![\begin{gathered} \bar{y}=\frac{\operatorname{\sum}_^y}{n} \\ \bar{y}=(106.5)/(10) \\ \bar{y}=10.65 \\ and \\ \bar{x}=\frac{\operatorname{\sum}_^x}{n} \\ \bar{x}=(666)/(10) \\ \bar{x}=66.6 \end{gathered}]()
Therefore,

Therefore,
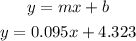
To the nearest tenth
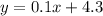
The least square method didn't give an accurate answer, so we use a graphing tool to estimate instead
Here
m = 0.5 (to the nearest tenth)
b = -23.5 (to the nearest tenth)
The answer is