From the given values, we know there are 2 defective resistors and 9 not defective. then, we have
![P(1\text{ defective)=}(C^9_3* C^2_1)/(C^(11)_4)]()
where
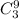
denote the combinations of 9 elements taking in 3, that is 3 good resistor from the 9 which are not defective. Similarly,

denotes the combinations of 2 elements taking in 1, that is, 1 defective resistor form the 2 defective resistors.
Then, we have
![P(1\text{ defective)=}(84*2)/(330)]()
then, the answer is
![P(1\text{ defective) =}0.509]()