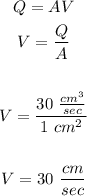ANSWER :
The answer is 30 cm/sec
EXPLANATION :
We have an inverted square pyramid with a square side of 7 cm and a height is 14 cm.
We need to find the area of the square at 2 cm from below.
Using similar triangles, we will express the side view as 2D :
We need to find the side of the square at 2 cm level.
The ratio of the sides of the smaller triangle and bigger triangle must be the same :
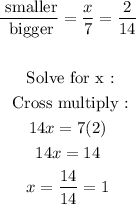
So the value of x is 1, then the side of the square at 2 cm level is 1 cm
The area of that square is :
A = 1 x 1 = 1 cm^2
The inverted pyramid is filled with water at a constant rate of Q = 30 cm^3 per second.
And we are asked to find the rate when the water level is 2 cm or when the area of the square is 1 cm^2 from the result we calculated above.
Recall the formula of rate :

We have the following :
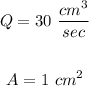
Using the formula above, the rate is :