The resistance R of a rod with length L, cross-sectional area A and resistivity ρ is given by:
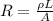
On the other hand, the area of a circle with diameter D is given by:
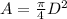
Then, the resistivity of the rod in terms of its diameter is:
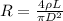
Replace L=2.96m, D=0.89cm and ρ=2.8×10^(-8)Ωm to find the resistance of the metal rod:
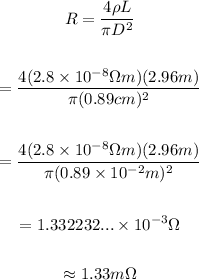
Therefore, the resistance of the metal rod is approximately 1.33 miliOhms.