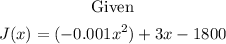
The given function in a quadratic function in standard form where
a = -0.001, b = 3, and c = -1800
It is a parabola that is facing downwards, therefore, the vertex of this parabola, (x,y) is the maximum of the function where
x is the amount of books that the author must sell for the most profit, and
y is the max profit per day.
We can find the vertex using
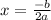
Substitute the following values, and we get

Now that we have x, plug it in the original function to solve for y
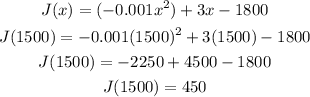
We have determine that the vertex of the function is at (1500,450). We can now conclude that
The max profit per day is $450.
The amount of of books the author must sell for the most profit is 1500 books.