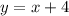Answer:
Part A:
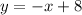
Part B:
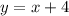
Explanation:
Part A:
Remember that two parallel lines have the same slope. This way, we can conclude that the slope of this particular line is:
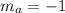
Since we already know that this line passes through point (2,6), we can use this point, the slope we've found and the slope-point form to get an equation for the line:

Therefore, we can conclude that the equation of this line is:
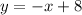
Part B:
Remember that the product between the slopes of two perpendicular lines is -1. This way, we'll have that:
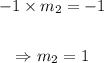
Since we already know that this line passes through point (2,6), we can use this point, the slope we've found and the slope-point form to get an equation for the line:
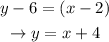
Therefore, we can conclude that the equation of this line is: