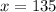
Step-by-step explanation
The formula for calculating the sum of interior angles in a polygon is ( n − 2 ) × 180 ∘ where is the number of sides.
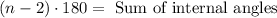
Step 1
find the sum of the internal angles in the given polygon
Let
number of sides = 8
Now, replace

Step 2
now, we have the other angles, so
sum of internal angles is:
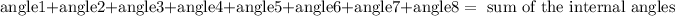
replace
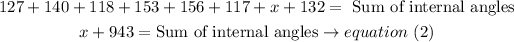
hence
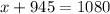
subtract 945 in both sides to solve for x
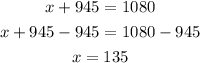
i hope this helps you