17 Liters
Step-by-step explanationStep 1
find the total area to paint
we need to assume the floor wont be painted, so the total are to paint is
the are of a rectangle is gieven by:
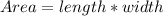
so, the total area will be

so , the area to paint is 680 square meters
Step 2
finally, to know the number of Liters need , divide the amount ( total area) by the rate of the paitn, so
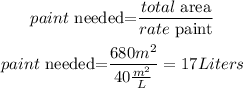
so, the total paint needes is 17 Liters, and paint comes in 1-L cans, so
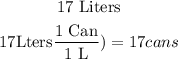
therefore, the answer is
17 Liters
I hope this helps you