Question

Find the vertex of the following equation: y = -5x² - 270x - 520

Answer 1

In order to find the vertex of this quadratic equation, first let's find the coefficients a, b and c from the standard form of the quadratic equation:

`y=ax^2+bx+c`

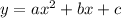
Comparing with the given equation, we have a = -5, b = -270 and c = -520.

Now, let's calculate the x-coordinate of the vertex using the formula below:

`\begin{gathered} x_v=(-b)/(2a) \\ x_v=(-(-270))/(2\cdot(-5)) \\ x_v=(270)/(-10) \\ x_v=-27 \end{gathered}`

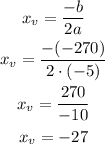
Using this value of x in the equation, we can find the y-coordinate of the vertex:

`\begin{gathered} y_v=-5x^2_v-270x_v-520 \\ y_v=-5\cdot(-27)^2-270\cdot(-27)-520 \\ y_v=-5\cdot729+7290-520 \\ y_v=-3645+7290-520 \\ y_v=3125 \end{gathered}`

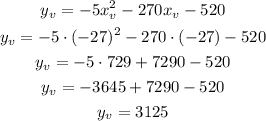
Therefore the vertex is located at (-27, 3125).