ANSWER:
456 square meters
Explanation:
The first thing is to represent the problem in the following figure:
To calculate the area of the part of the circle outside of the square, we must calculate the area of the circle and subtract the area of the inscribed square.
To calculate the area of the square, we plant the following, taking into account that the diagonal of the square is equal to twice the radius and the sides equal to the radius times the root of two, like this:
Knowing the value of the side of the square, we can directly calculate the area of the part of the circle outside of the square, subtracting the corresponding areas like this:
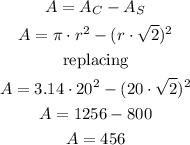
The area of the part of the circle outside of the square is equal to 456 square meters