Question

Use the quadratic function fly)=-22 +53411 to answer the following questions,a) Use the vertex formula to determine the vertes.The verteris(Type an ordered pair Simplify your answer.)

Answer 1

The vertex of a quadratic function can be found by using the following expression:

`x=(-b)/(2a)`

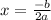
Where "a" is the number multiplying x² and b is the number multiplying x. For this function a = -2 and b = 5. Applying these on the problem we have:

`x=(-5)/(2\cdot(-2))=(-5)/(-4)=(5)/(4)=1.25`

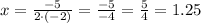
To find the y coordinate of the vertex we need to use the value for x that we found above. We have:

`\begin{gathered} f(x)=-2x^2+5x+11 \\ f((5)/(4))=-2\cdot((5)/(4))^2+5\cdot((5)/(4))+11 \\ f((5)/(4))=-2(25)/(16)+(25)/(4)+11 \\ f((5)/(4))=(-50)/(16)+(25)/(4)+11 \\ f((5)/(4))=-3.125+6.25+11=14.125 \end{gathered}`

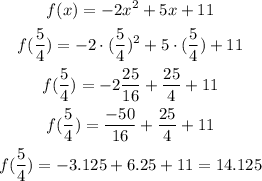
The ordered pair for this function's vertex is (1.25, 14.125)