SOLUTION
From the image above
![\begin{gathered} z^2=6^2+3^2\ldots\text{ by pythagora's rule } \\ z^2=36+9 \\ z^2=45 \\ z=\sqrt[]{45} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/8xtntf1muvceggz1ajxdet4vwuub2mna06.png)
Considering the bigger right angle triangle,
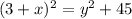
We can obtain the expression of y from the smaller right angle triangle,
Using pythagora's rule, we have
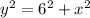
Then, recall
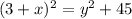
Substite the expression for y², we have
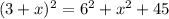
Expand the paranthesis, we have
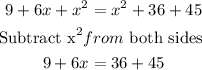
subtract 9 from both sides, we have
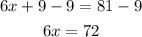
Divide both sides by 6, we obtain
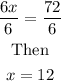
Therefore
Answer: x= 12