Question

The Connecticut River flows at a rate of 6 km / hour for the length of a popular scenic route. If a cruiser to travels 3 hours with the current to reach a drop-off point, but the return trip against the same current took 7 hours. Find the speed of the boat without a current?The speed of the boat without a current is ____ km/hour. (if needed, round to 2 decimal places).

Answer 1

Given:

Speed of current (y)= 6 km/hour

Distance = d km

Speed of boat in still water = x km/hour

Speed of the cruiser with the current= (x+6) km/hour

Speed of the cruiser against the current= (x-6) km/hour

`\text{Time to travel with the stream=}(d)/(x+6)`
`3=(d)/(x+6)`
`3\mleft(x+6\mright)=d`
`d=3x+18\ldots.\text{ (1)}`
`\text{Time to travel }against\text{ the stream=}(d)/(x-6)`
`7=(d)/(x-6)`
`d=7x-42\ldots.\text{ (2)}`

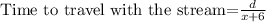
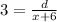
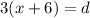
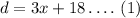
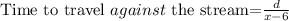
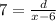
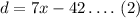
From equation (1) and (2)

`7x-42=3x+18`
`7x-3x=18+42`
`4x=60`
`x=15`

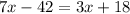
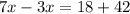
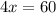
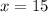
Therefore the speed of the without a current is 15km/hour.