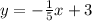Question

Through: (-5,4) perpendicular to x=5

Answer 1

First let's calculate the slope of the straight line

For slopes that are perpendicular to each other we can use the following formula

`m1m2=-1`

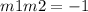
Where

m1 = original slope

m2 = perpendicular slope

`\begin{gathered} m2=-(1)/(m1) \\ m2=-(1)/(5) \end{gathered}`

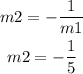
Now for the intersection

`\begin{gathered} b=y-mx \\ b=4-((-1)/(5))\cdot(-5) \\ b=4-1 \\ b=3 \end{gathered}`

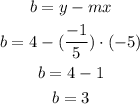
The equation of the line that passes through the point (-5,4) with a slope of -1/5 is

`y=-(1)/(5)x+3`