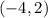Question

What does it mean translate the figure 5 units up

Answer 1

By definition. a Translation is a transformation in which a figure is moved a fixed distance in a fixed direction.

The Image is the figure obtained after the transformation and the Pre-Image is the original figure.

In this case, you know that the figure shown in the picture must be translated 5 units up. Therefore, the rule for this transformation is:

`(x,y)\rightarrow(x,y+5)`

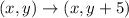
You can identify that the marked point on the Pre-Image has the following coordinates:

`\mleft(-4,-3\mright)`

Therefore, applying the rule for this transformation, you get that the coordinates of the marked point in the final figure, are:

`\mleft(-4,-3\mright)\rightarrow\mleft(-4,-3+5\mright)\rightarrow(-4,2)`

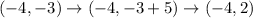
The answer is:

Coordinates of the marked point in the original figure:

`(-4,-3)`

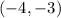
Coordinates of the marked point in the final figure:

`\mleft(-4,2\mright)`