Question

1(c). What is a better deal? Explain. Deal 1: 2 mediums 14'' (round) pizza for $14 total Deal 2: 1 large 20'' (round) pizza for $13 total

Answer 1

To get the better deal of the two, we need to find the cost per area of pizza for each deal and compare.

Deal 1: 2 medium 14'' (round) pizza for $14 total

The area of a circle is calculated as

`A=\pi r^2`

where r is the radius.

The area of the pizza is calculated to be:

`\begin{gathered} r=14 \\ \therefore \\ A_1=\pi*14^2=196\pi \end{gathered}`

Hence, the total area for the two pizzas will be:

`\Rightarrow196\pi*2=392\pi`

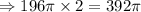
The cost per square inch of pizza is, therefore, calculated to be:

`\Rightarrow(14)/(392\pi)=0.011`

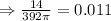
The pizza costs $0.011 per square inch.

Deal 2: 1 large 20'' (round) pizza for $13 total

The area of the pizza is calculated to be:

`\begin{gathered} r=20 \\ \therefore \\ A_2=\pi*20^2=400\pi \end{gathered}`

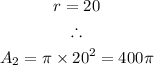
Hence, the cost per square inch of pizza is calculated to be:

`\Rightarrow(13)/(400\pi)=0.010`

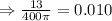
The pizza costs $0.010 per square inch.

CONCLUSION:

The better deal will be the deal with the lesser cost per square inch. As can be seen from the calculation, both deals are about the same price per square inch if approximated. However, without approximation, Deal 2 has a slightly lesser cost per square inch.

Therefore, DEAL 2 IS THE BETTER DEAL.