Question

Define a variable, used let statements, set up an equation, then solve. Morgan is making two cookie recipes. Recipe A calls for one-third third less than twice the number of cups of sugar that Recipe B calls for. If she needs four and one-sixths cups of sugar in all, how many cups will she need for Recipe A?

Answer 1

Step-by-step explanation

Let's see the facts:

-Morgan is making ----------------> 2 cookie recipes.

Recipe A ---> A = 2RecipeB -(1/3) 2RecipeB

-She needs-----------> Recipe A + Recipe B = 4 1/6 cups of sugar

Now, we have a system of equations:

(1) A = 2B -(1/3)2B

(2) A + B = 4 1/6

Multiplying both sides of (1) by 3:

3A = 6B - B

Simplifying:

3A = 5B

Isolating B:

B = 3/5 A

Substituting B-value in (2)

`A\text{ + }(3)/(5)A\text{ = 4}(1)/(6)`

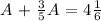
Reordering:

`A+(3)/(5)A=\text{ }(25)/(6)`

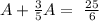
Multiplying both sides by 30:

`30A\text{ + 18A = 25}\cdot5`
`48A\text{ = 125}`

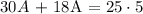
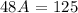
Dividing both sides by 48:

`A\text{ = }(125)/(48)`

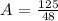
Representing as mix fraction and rounding:

`A=\text{ 2}(2)/(3)`

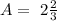
ANSWER: She will need two and two-thirds cups of Recipe A.