Question

A population of a certain species of bird is 22,000 animals and is decreasing by 700 birds per year..Write an equation for y, the population at time t (in years), representing the situation.y= How many birds are in the population after 7 years?

Answer 1

We can solve that problem using a linear function, we know that

`y=mx+y_0`

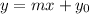
Where y0 is the initial population and m is the rate of decreasing, we know that for each "x" years we have -700 birds, therefore

`y=-700x+22000`

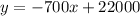
Let's use t instead of x

`y=-700t+22000`

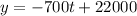
That's the equation that represents the population at time t

`\begin{gathered} y=-700t+22000\text{ \lparen t = 7\rparen} \\ \\ y=-700\cdot(7)+22000 \\ \\ y=-4900+22000 \\ \\ y=17100 \end{gathered}`

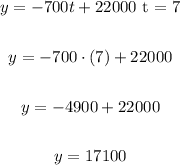
Therefore after 7 years, the population will be 17100 birds.