Since J is the midpoint of the CT segment, then:
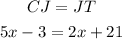
Now, you can solve the equation for x:
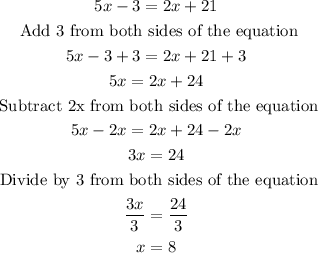
Replace the value of x into the equation for segment CJ or segment JT to find out what its measure is. For example in the equation of the segment CJ:
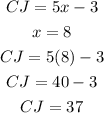
Finally, you have
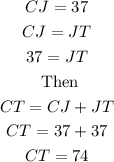
Therefore, the measure of the segment CT is 74.