1 Answer

Bud · Answer 1 · 2023-06-01T21:15:00+0000

The Solution.

By formula, the volume of the planet (sphere) is given as below:

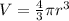
$V=(4)/(3)\pi r^3$

In this case,

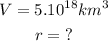
$\begin{gathered} V=5.10^(18)km^3 \\ r=\text{?} \end{gathered}$

Substitting these given values into the formula above, we can solve for r, the radius of the planet.

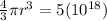
$(4)/(3)\pi r^3=5(10^(18))$

Dividing both sides by

$(4)/(3)\pi$

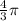
We get

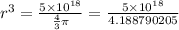
$r^3=(5*10^(18))/((4)/(3)\pi)=(5*10^(18))/(4.188790205)$

Taking the cube root of both sides, we have

$\begin{gathered} r=\sqrt[3]{(}(5*10^(18))/(4.188790205))=(1.060784418*10^6)km^{} \\ Or \\ r=1060784.418\text{ km} \end{gathered}$

Thus, the correct answer is 1060784.418km.

Please log in or register to add a comment.