Question

I don’t really need explanation just give answer honestly I will rate you a 5star regardless I thankyou so much for the help!

Answer 1

Step-by-step explanation

The information given directly by the picture is that:

`\begin{gathered} CG\cong CH \\ \angle G\cong\angle H \end{gathered}`

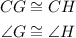
This means we have a pair of congruent sides and a pair of congruent angles.

We need one more information to prove congruency. There is no way of getting side information, by if we see the vertex C, the angles make a pair of vertical angles. Vertical angles are congruent, so:

`\angle FCG\cong\angle JCH`

This means now that we have 2 pairs of congruent angles and one pair of congruent sides, so we will use either AAS or ASA.

To determine which is the case, we can visualize the order in which the angles and side appear going around the triangle.

We can see that we have an Angle then the side then the other Angle, so the order is Angle-Side -Angle, so the rule we need to use is ASA.

Answer

Angle-Side-Anlge, that is ASA.