Question

4. What common characteristics will two parabolas in the family f(×) = a(× - 4)(× - 8) have?

Answer 1

• The Same roots

,

• The same axis of symmetry

1) If we compare two parabolas from this family, like:

`\begin{gathered} f(x)=-1(x-4)(x-8) \\ g(x)=2(x-4)(x-8) \end{gathered}`

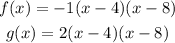
Note that the difference is in the leading coefficient "a".

2) Both parabolas will have the same roots, the same x-intercepts:

`x_1=4,x_2=8`

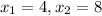
In addition to this, we can state that both will share the same axis of symmetry:

`\begin{gathered} f(x)=-1(x-4)(x-8) \\ f(x)=\quad -x^2+12x-32_{} \\ h=(-12)/(2(-1))=6 \end{gathered}`

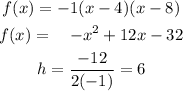
As well as:

`\begin{gathered} g(x)=2(x-4)(x-8) \\ g(x)=2x^2-24x+64 \\ h=(24)/(2(2))=6 \end{gathered}`

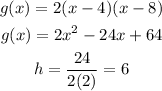
Hence, the answer is:

0. Same roots

,

1. Same axis of symmetry