We will have the following:
First, we recall that the simple interest formula is given by:
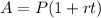
Now, for the accounts that are described in the problem we will have that:
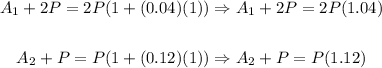
Now, we have that:
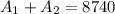
Then:
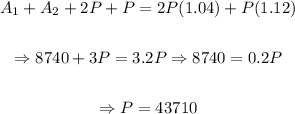
So, the amount invested at 4% interest is $87 420.
And, the amount invested at 12% interest is $43 710.