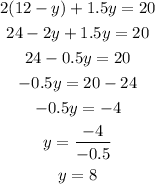Question

Consumer Economics Each family in a neighborhood is contributing $20 worth of food to the neighborhood picnic. The Harlin family is bringing 12 packages of buns. The hamburger buns cost $2.00 per package. The hot-dog buns cost $1.50 per package. How many packages of each type of bun did they buy?Choose the correct equation that represents the number of buns purchased. [ Select ]Choose the correct equation that represents the cost of the buns. [ Select ][ Select ] packages of hamburger buns were bought.[ Select ] packages of hot dog buns were bought.

Answer 1

Step-by-step explanation

In the question, we are given some important details to work with. Here is a list of them.

1) First, we must note that each family is contributing $20 worth of food.

2) Harlin's family brought 12 packages to the party.

3) The 12 packages consist of two types of buns namely hamburgers and hot dogs. The hamburger buns cost $2 per package while the hot-dog buns cost $1.50

Part A

Let's assume that the number of hamburger packages represents x and the number of hot dogs packages represents y. We can conclude that the sum of bought packages should be equal to 12. We can then translate this information into the equation below.

`x+y=12`

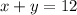
Answer A: x+y = 12

Part B

Now, we can figure out the equation that represents the cost of the buns. Since we know the cost of each buns package, we can multiply the cost of each buns package by the number of packages that were brought to the party by the Harlin family.

Also, we will add the resulting expressions and equate it to the cost of the worth of food each family will bring to the party.

Therefore,

`\begin{gathered} Total\text{ cost of hamburgers = }2* x=2x \\ Total\text{ cost of Hot dogs = 1.50 x y =1.5y} \\ \therefore\text{Tota cost of buns }\Rightarrow\text{ }2x+1.5y=20 \\ \\ \end{gathered}`

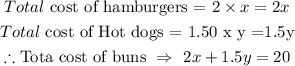
Answer B: 2x+1.5y = 20

Part C And Part D

The above sections can be gotten by solving the previous systems of equations simultaneously. Therfore,

`\begin{gathered} x+y=12\text{ -----1} \\ 2x+1.5y\text{ =20 -----2} \end{gathered}`

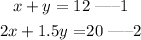
Let's create equation three from equation 1

`x=12-y-----3`

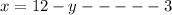
Then we will substitute equation three into the untouched equation 2

`\begin{gathered} 2(12-y)+1.5y=20 \\ 24-2y+1.5y=20 \\ 24-0.5y=20 \\ -0.5y=20-24 \\ -0.5y=-4 \\ y=(-4)/(-0.5) \\ y=8 \end{gathered}`