a. A 90% confidence interval for the population proportion is [0.6286, 0.6914].
b. A 95% confidence interval for the population proportion is [0.6226, 0.6974].
In Mathematics and Statistics, the sample proportion of a sample can be calculated by using this formula:
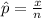
Where:
- x represent the total number of individuals that are having a specified characteristic.
- n represent the total number of individuals that are in the sample.
Part a.
For a confidence level of 90%, the critical value of z is given by;
Critical value, z* = 1.645
Now, we can calculate the confidence interval (CI) by using the following formula;

CI = [0.66 ± 1.645(0.0191)]
CI = [0.66 ± 0.0314]
CI = [0.66 - 0.0314, 0.66 + 0.0314]
CI = [0.6286, 0.6914]
Part b.
For a confidence level of 95%, the critical value of z is given by;
Critical value, z* = 1.960
Now, we can calculate the confidence interval (CI) by using the following formula;
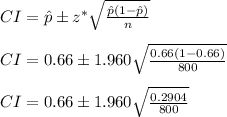
CI = [0.66 ± 1.960(0.0191)]
CI = [0.66 ± 0.0374]
CI = [0.66 - 0.0374, 0.66 + 0.0374]
CI = [0.6226, 0.6974]