Given, the perimeter of the rectangular billboard, P=42 m.
The length of the rectangular billboard is 9 m more than the width.
Let l be the length and w be the width of the rectangular billboard.
Then, the length can be expressed as,
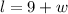
The perimeter of a rectangle can be expressed as,
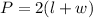
Now, put l=9+w and P=42 m in the above equation to find w.
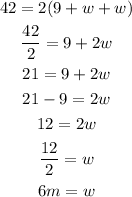
Hence, the length is,
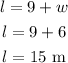
Therefore, the length of the rectangular billboard is 15 m and the width of the rectangular billboard is 6 m.