Question

Write a function to model the geometric sequence in the table. n: (1 2 3 4 5)a: (75 15 3 3/5 3/25)a) f(n) = 75 (1/5) nb) f(n) = 75 (1/5) n-1c) f(n) = 1/5 (75) nd) f(n) = 1/5 (75) n-1

Answer 1

First let's find the ratio of the sequence, by dividing one term by the term before:

`\begin{gathered} \text{second term: 15} \\ \text{first term: 75} \\ ratio=(15)/(75)=(1)/(5) \end{gathered}`

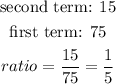
So the ratio is 1/5 and the first term is 75.

Now, we can use the following formula for the nth term of a geometric sequence:

`a_n=a_1\cdot q^(n-1)`

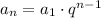
Where q is the ratio and a1 is the first term. So we have:

`a_n=75((1)/(5))^(n-1)`

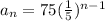
Substituting an by the function f(n), we have:

`f(n)=75((1)/(5))^(n-1)`

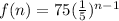
So the correct option is b)