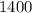Solution:
The cuboid is a solid-shaped figure formed by six faces. A cuboid is a simple figure. It has three dimensions - width, length, and height. Thus, the cuboid is a parallelepiped. Now, the surface area of the parallelepiped is the sum of the areas of all sides, that is:
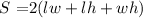
where
l is the lenght
w is the width
and
h is the height
According to the figure given in the problem, we have that:
l = 30
w = 10
h = 10
thus, the surface area of the given cuboid would be:
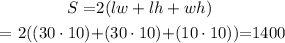
So that, we can conclude that the correct answer is: