Knowing that
- The number of classified documents has increased linearly.
- In 2001 there were 8.2 million documents.
- In 2005 there were 17.4 million documents.
- The variable "n" represents the number of documents (in millions) labeled as classified.
- The variable "t" represents the number of years since 2000.
The Slope-Intercept Form of the equation of a line is:

Where "m" is the slope and "b" is the y-intercept.
The slope of a line can be found using this formula:
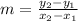
Where these two points are on the line:
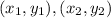
In this case, you know these two points:
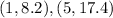
Then, you can substitute values into the formula and find the slope of the line:
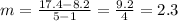
Now you know that the form of the equation is:
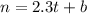
In order to find "b", you need to:
- Choose one of the points on the line:
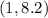
- Identify the value of each variable. Notice that:
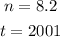
- Substitute those values of "n" and "t", and the slope into the equation:
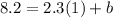
- Solve for "b":
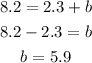
Therefore the equation of the Linear Model is:
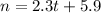
Hence, the answer is: Option D.