Question

Determine the values of m and n in the polynomial 2x* + mx -x + n such that the binomial (x - 1) is a factor and that the remainder when divided by (x + 2) is -18.

Answer 1

The remainder theorem of polynomials states: if a polynomial p(x) is divided by a binomial (x - a), the remainder obtained is p(a).

In this case, the polynomial is:

`p(x)=2x^4+mx^3-x^2+n`

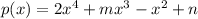
Applying the remainder theorem p(-2) = -18, that is:

`\begin{gathered} p(-2)=2\cdot(-2)^4+m\cdot(-2)^3-(-2)^2+n \\ -18=2\cdot16+m\cdot(-8)-4+n \\ -18=32-8m-4+n \\ -18-32+4=-8m+n \\ -46=-8m+n\text{ (eq. 1)} \end{gathered}`

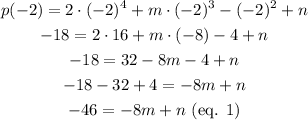
Given that (x - 1) is a factor, then p(1) = 0, that is:

`\begin{gathered} p(1)=2\cdot1^4+m\cdot1^3-1^2+n \\ 0=2+m-1+n \\ -2+1=m+n \\ -1=m+n\text{ (eq. 2)} \end{gathered}`

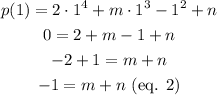
Now, we have a system of 2 equations and 2 variables: m and n. Subtracting equation 2 to equation 1, we get:

-8m + n = -46

-

m + n = -1

------------------------

-9m = -45

m = (-45)/(-9)

m = 5

Substituting this result into equation 2, we get:

5 + n = -1

n = -1 - 5

n = -6