Question

In isosceles △ABC where AC≅BC, altitiude CD is drawn. If AC= 17 and AB= 30. Determine the altitiude of the triangle.

Answer 1

By definition, an Isosceles triangle is a triangle that have two congruent sides, and the altitude divides the triangle into two equal Right triangles.

Remember that a Right triangle is a triangle that has an angle whose measure is 90 degrees.

Based on this, you know that:

`\begin{gathered} AD=BD=(AB)/(2) \\ \\ AC=BC \end{gathered}`

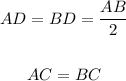
Knowing that:

`\begin{gathered} AB=30 \\ AC=17 \end{gathered}`

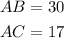
You get that:

`\begin{gathered} AD=BD=(30)/(2)=15 \\ \\ AC=BC=17 \end{gathered}`

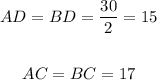
The Pythagorean Theorem states that:

`a^2=b^2+c^2`

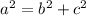
Where "a" is the hypotenuse and "b" and "c" are the legs of the right triangle.

So you can identify that, for this case:

`\begin{gathered} a=17 \\ b=15 \\ c=CD \end{gathered}`

Where "CD" is the altitude of the triangle.

Therefore, substituting values and solving for "CD", you get this result:

`\begin{gathered} 17^2=15^2+CD^2 \\ \sqrt[]{17^2-15^2}=CD \\ CD=8 \end{gathered}`

The answer is: Option (1)