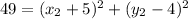Question

Using the point (-5, 4) has one endpoint, State a possible location of the other endpoint given the line segment is 7 units long. Apply the distance formula to create a possible endpoint(s) from a given location.

Answer 1

Step-by-step explanation

Since the line segment is 7 units long, we can apply the following relationship:

(x_1+ 7 , y_1) = (x_2 , y_2)

`(-5+7)=2`

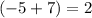
The coordinate of the endpoint is as follows:

`(x_(endpoint),y_(endpoint))=(2,4)`

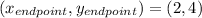
We can get to this point by applying the distance formula as follows:

`distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

Applying the square power to both sides:

`7^2=(x_2-(-5))^2+(y_2-4)^2`

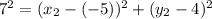
Subtracting numbers:

`49=(x_2+5)^2+(y_2-4)^2`

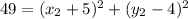
Now, if the x_2 coordinate is -3, the value of y_2 will be as follows:

`49=(-3+5)^2+(y_2-4)^2`
`49=4+(y_2-4)^2`

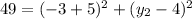
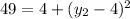
Subtracting -4 to both sides:

`45=(y_2-4)^2`

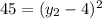
Applying the square root to both sides:

`√(45)=y_2-4`

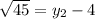
Adding +4 to both sides:

`4+√(45)=y_2`

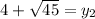
In conclusion, the equation to get the coordinate from a given point is,

`49=(x_(2)+5)^(2)+(y_(2)-4)^(2)`