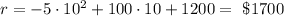If Mr. Stern charges a monthly rent of $200, we still can rent all suites. An average increase of $5 in the monthly rent imply in the addition of one suite vacant.
Therefore, the total monthly revenue r in function of the number of vacant units v can be writen in the form:

The monthly rent m is given by:
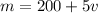
The value of v that maximize the total revenue r is the one found in the vertex of the parabola that represents r:
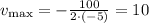
Therefore, the monthly rent that maximize the total revenue is m = 200 + 5*10 = $700
The monthly revenue with this monthly rent is: