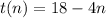We need to find the explicit equation for the sequence:
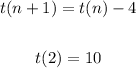
First, we can complete the given table. Notice that when we subtract 4 from the n-th term, we obtain the next term (n+1).
Then, to find a previous term, we can add 4. Thus. we obtain:
n t(n)
0 14+4 = 18
1 10+4 = 14
2 10
3 10-4 = 6
4 6-4 = 2
5 2-4 = -2
Now, observing the above relations, we need to write an expression for t(n) in terms of n:
n t(n)
0 18 = 18 - 0*4
1 14 = 18 - 1*4
2 10 = 18 - 2*4
3 6 = 18 - 3*4
4 2 = 18 - 4*4
5 -2 = 18 - 5*4
...
n 18 - n*4
Therefore, an explicit equation for the sequence is: