Question

Find the equation of the axis of symmetry of the following parabola algebraically. y=x²-14x+45

Answer 1

x = 7, y = -4

(7, -4)

Step-by-step explanation:

Given the below quadratic equation;

`y=x^2-14x+45`

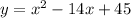
To find the equation of the axis of symmetry, we'll use the below formula;

`x=(-b)/(2a)`

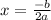
If we compare the given equation with the standard form of a quadratic equation, y = ax^2 + bx + c, we can see that a = 1, b = -14, and c = 45.

So let's go ahead and substitute the above values into our equation of the axis of symmetry;

`\begin{gathered} x=(-(-14))/(2(1)) \\ =(14)/(2) \\ \therefore x=7 \end{gathered}`

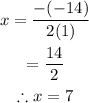
To find the y-coordinate, we have to substitute the value of x into our given equation;

`\begin{gathered} y=7^2-14(7)+45 \\ =49-98+45 \\ \therefore y=-4 \end{gathered}`