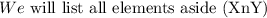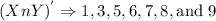Question

2. The Venn diagram shows the sets U, X and Y.UXY.34 246..9.512:31List the elements of the following sets:(a) X(b) Y(c) U(d) XUY(e) XnY(g) X\Y(h) Y\X(f) X'(1) (XY)2:31

Answer 1

Given the Venn diagram in the question, we can proceed to answer the questions as follow

`\begin{gathered} X=\text{members of the subset X} \\ This\text{ gives: 1,2,3,4, and 5} \end{gathered}`
`\begin{gathered} QuestionA\text{ } \\ X=1,2,3,4,and\text{ 5} \\ \end{gathered}`

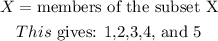
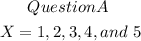
Question B

Y= members of subset Y

Y =2,4,6, and 8

Question C

U means that we should list all elements in the universal set

U = ALL members of the set

U = 1,2,3,4,5,6,7,8, and 9

Question D

This is the union of both sets X and Y. This means we will list all the members that are found in the 2 subsets

`\text{XUY}=1,2,3,4,5,6,\text{ and 8}`

Question E

`\begin{gathered} \text{XnY means we are to find the elements that are common to both X and Y} \\ \text{XnY}=2\text{ and 4} \end{gathered}`

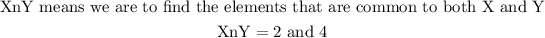
Question F

X' means that we should find all members of the set except that of X

`X^(\prime)=6,7,8,\text{ and 9}`

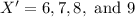
Question G

X\Y means that we should list the elements of X that are not found in Y

X\Y= 1,3, and 5

Question H

Y\X means that we should list the elements of Y that are not found in X

Y\X= 6, and 7

Question I

To solve (XnY)' we will follow the steps below

Step 1: Find (XnY)

`\text{XnY}=2\text{ and 4}`

Step 2: Find (XnY)'

`We\text{ will list all elements aside (XnY)}`
`(XnY)^{^(\prime)}\Rightarrow1,3,5,6,7,8,\text{and 9}`