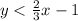To identify the inequality of the given graph:
1. Identify the equation of the borderline in slope-intercept form (y=mx+b)
- Find the slope (m): Use two points in the line in the next formula:
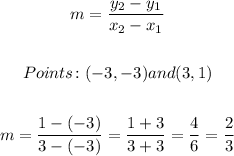
- Identify the y-intercept (b): the value of y where the line cross the y-axis (when x is 0)
b= -1
Equation of the border line:
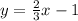
2, Identifify the inequality sing:
-When the inequality is < or > the borderline is a dotted line
-When the inequality is ≥ or ≤ the border line is a full line
-When the inequality is < or ≤ the shaded area is under the borderline
-When the inequality is > or ≥ the shaded are is over the borderline
In this case you have a dotted borderline and a shaded area under the borderline, then, the inequality is: