Question

Imagine you are four years old. A rich aunt wants to provide for your future. She hasoffered to do one of two things.Option 1: She would give you $1000.50 a year until you are twenty-one.Option 2: She would give you $1 this year, $2 next year, and so on, doubling the amounteach year until you were 21.If you only received money for ten years, which option would give you the most money?

Answer 1

Given the situation to model the arithmetic and the geometric sequences.

Imagine you are four years old. A rich aunt wants to provide for your future. She has offered to do one of two things.

Option 1: She would give you $1000.50 a year until you are twenty-one.

This option represents the arithmetic sequence

The first term = a = 1000.50

The common difference = d = 1000.50

The general formula will be as follows:

`\begin{gathered} a_n=a+d(n-1) \\ a_n=1000.50+1000.50(n-1) \\ \end{gathered}`

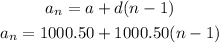
Simplify the expression:

`a_n=1000.50n`

Option 2: She would give you $1 this year, $2 next year, and so on, doubling the amount each year until you were 21.

This option represents the geometric sequence

The first term = a = 1

The common ratio = r = 2/1 = 2

The general formula will be as follows:

`\begin{gathered} a_n=a\cdot r^(n-1) \\ a_n=1\cdot2^(n-1) \end{gathered}`

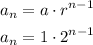
Now, we will compare the options:

The first term of both options is when you are four years old that n = 1

you only received money for ten years so, n = 10

So, substitute with n = 10 into both formulas:

`\begin{gathered} Option1\rightarrow a_(10)=1000.50(10)=10005 \\ Option2\rightarrow a_(10)=1\cdot2^(10-1)=2^9=512 \end{gathered}`

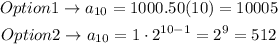
So, the answer will be:

For ten years, the option that gives the most money = Option 1