Question

a1. The amount of milk in a one-gallon milk container has a normal distribution with a meanof 1.07 gallons and a standard deviation of 0.12 gallons.Calculate and interpret the z-score for exactly one gallon of milk.

Answer 1

The z-score formula is given to be:

`z=(x-\mu)/(\sigma)`

where

`\begin{gathered} x=score \\ \mu=mean \\ \sigma=standard\text{ }deviation \end{gathered}`

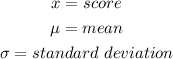
From the question given, the mean and standard deviations are provided as:

`\begin{gathered} \mu=1.07 \\ \sigma=0.12 \end{gathered}`

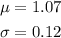
Therefore, the z-score of exactly 1 gallon is calculated to be:

`\begin{gathered} x=1 \\ \therefore \\ z=(1-1.07)/(0.12)=(-0.07)/(0.12) \\ z=-0.583 \end{gathered}`

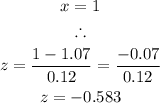
Therefore, the z-score is -0.583.

This tells us that a container with exactly one gallon of milk lies 0.583 standard deviations below the mean.