The simultaneous equations are:
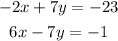
Since, the unknown y has the same co-efficient across the two(2) equations, we can eliminate it directly.
Thus, we have:
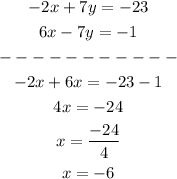
To find y, substitute for x = -6 into any of the equations.
Thus, we have:
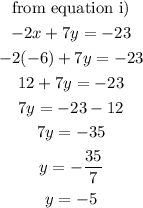
Hence, the correct option is option A