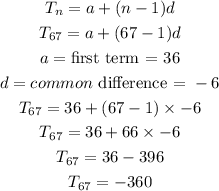Question

10. Determine if the following sequence is arithmetic or geometric. Then, find the 67th term. 36, 30, 24, 18, ... a. arithmetic, -360 b. arithmetic, 12 c. geometric, -360 d. geometric, 12

Answer 1

hello

to determine if the sequence is arthimetic or a geometric progression, we check if a common difference or common ratio exists between the two sequence

the sequence is 36, 30, 24, 18,......

from careful observation, this is an arthimetic progression because a common difference exists between them

d = 30 - 36 = -6

or

d = 24 - 30 = -6

to find the 67th term, let's apply the formula

`\begin{gathered} T_n=a+(n-1)d \\ T_(67)=a+(67-1)d \\ a=\text{first term = 36} \\ d=common\text{ difference = }-6 \\ T_(67)=36+(67-1)*-6 \\ T_(67)=36+66*-6 \\ T_(67)=36-396 \\ T_(67)=-360 \end{gathered}`