Recall that a function is continuous at a point if the limit as the variable approaches a value is the same as the value of the function at that point.
Now, notice that, using the definition of the function:
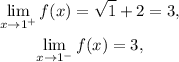
therefore:
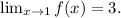
Given that the limit and the value of the function at x=1 are equal, the function is continuous at x=1.
Answer: It is continuous at x=1.